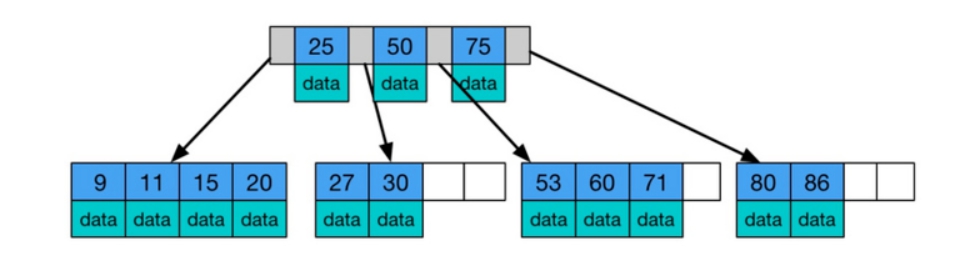
Tree --- B-Tree
Written on July 22nd , 2018 by Richard Lin
B-Tree
一個B-Tree為Degree M(Order M)代表:
- 每個Node有最多m個children。
- 一個non-leaf node若有k children代表他有k-1 keys。(因為必須要有k-1個keys才能生出k個children)
- root最少要有兩個children(代表說root至少要有1個key),如果他不是leaf node。
- 所以 non-leaf node(除了root)都至少有roof(m/2)個children。
- 所有leaf要出現在同一層。
- Node都會有key的上限與下限數量,上限就會是Degree,而下限通常會是t>=2,又被稱作minimum degree。
Insert value
透過key我們會自行搜尋出能夠放置key的地方,可是可能會遇到兩種情況,第一種是這個node有地方可以放(代表說這個node的key數量小於m-1),又或者是第二種這個node沒有地方可以放。
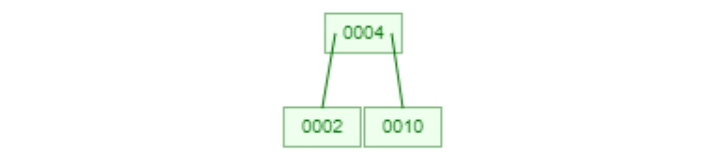
第一種情況我們會先在每個node看有沒有位置可以放,例如要插入5並且情況向下圖一樣。這時候我們可以放心的插入在4跟10中間。
 可是如果是下面這種情況,比4大的地方已經有往下長一個leaf node了。
可是如果是下面這種情況,比4大的地方已經有往下長一個leaf node了。
 所以我們變成要插入在10的左邊。
所以我們變成要插入在10的左邊。
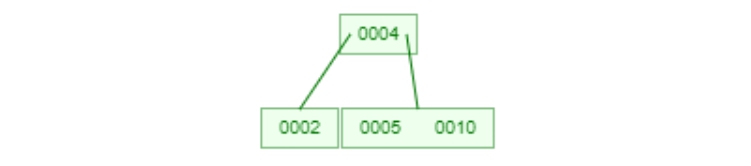
第二種情況就會啟動B-Tree的特殊機制就是在已經滿的node中選擇中間的數字(若中間有兩個就隨機選一個)來promote到node的上一層裡面,並把原本的node分成兩部分。
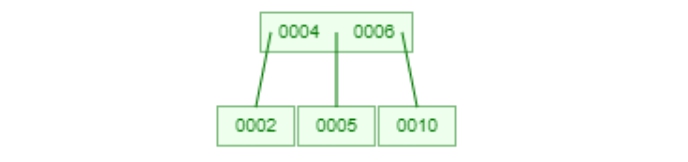
像是下圖我們是Degree=3的B-Tree,這時候如果我們要插入6進去的話,會造成[5 6 10]這個Node塞滿。
 所以我們會把這個Node拆成左、右兩個並把中間的6 promote上去。
所以我們會把這個Node拆成左、右兩個並把中間的6 promote上去。
 (動畫網址)[https://www.cs.usfca.edu/~galles/visualization/BTree.html]
(動畫網址)[https://www.cs.usfca.edu/~galles/visualization/BTree.html]
Delet value
這裡有很多種情況,假如今天我們要刪除X這個key。
- 如果這個Key在leaf node且刪掉這個key不會造成這個node不見,漂亮我們沒有對結構造成任何影響,所以我們就直接刪掉。
 刪除10。
刪除10。
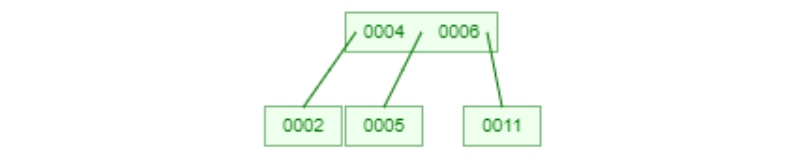
- 如果這個Key在leaf node但是我們刪掉他的話這個node會消失這時候我們就改變結構了。這時候我們會下放上層的node key(指標往上看的左邊或右邊的key都可以),將他降階到下面。
2-1.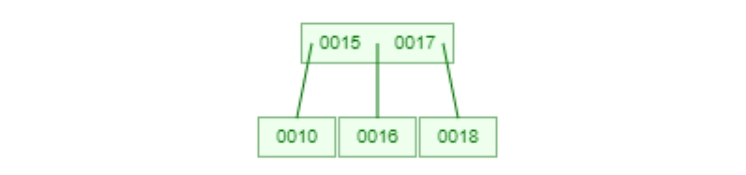 刪除18,降階17到16的node。
刪除18,降階17到16的node。
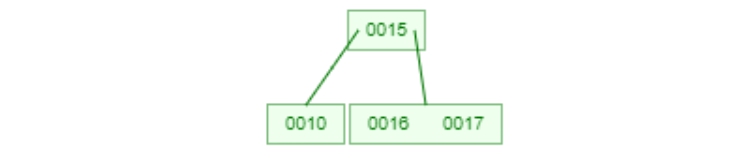 但是如過降階下去遇到node滿了的話怎麼辦,其實就跟insert的時候一樣把它拆成左右後promote中間的key到面的node。
但是如過降階下去遇到node滿了的話怎麼辦,其實就跟insert的時候一樣把它拆成左右後promote中間的key到面的node。
2-2. 如果左右的兄弟都沒有足夠的key給你的話,我們就必須執行merge。下面的tree定義是每個node不能少於2個key。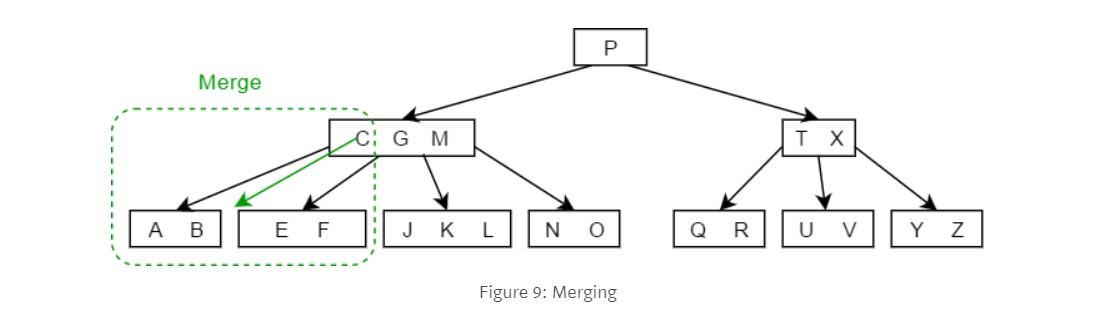 Merge成功,刪除B。
Merge成功,刪除B。
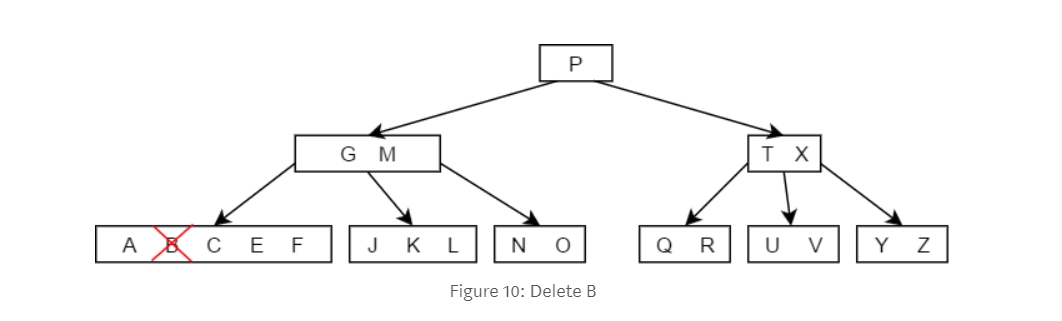
- 如果這個Key不在leaf node,那這時候我們一定有改變到數的結構,這樣我們一定要做些事情。
3-1. 往左子node找最大值或往右子node找最小值,如果有的話就將他代替自己。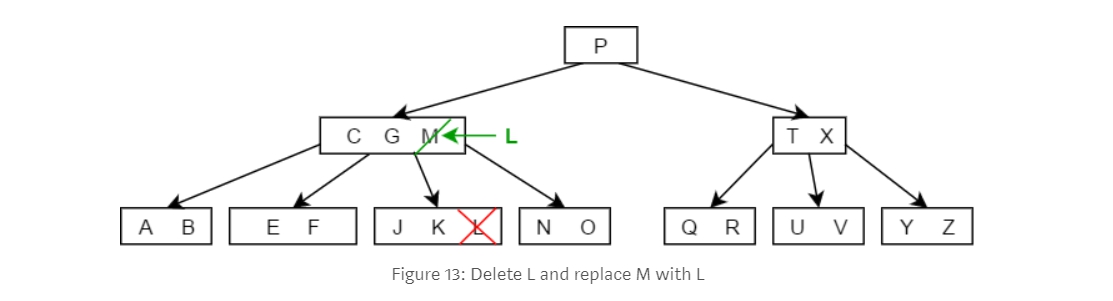 3-2. 如果都沒有的話就Merge左右兩個node再把自己刪除。
3-2. 如果都沒有的話就Merge左右兩個node再把自己刪除。
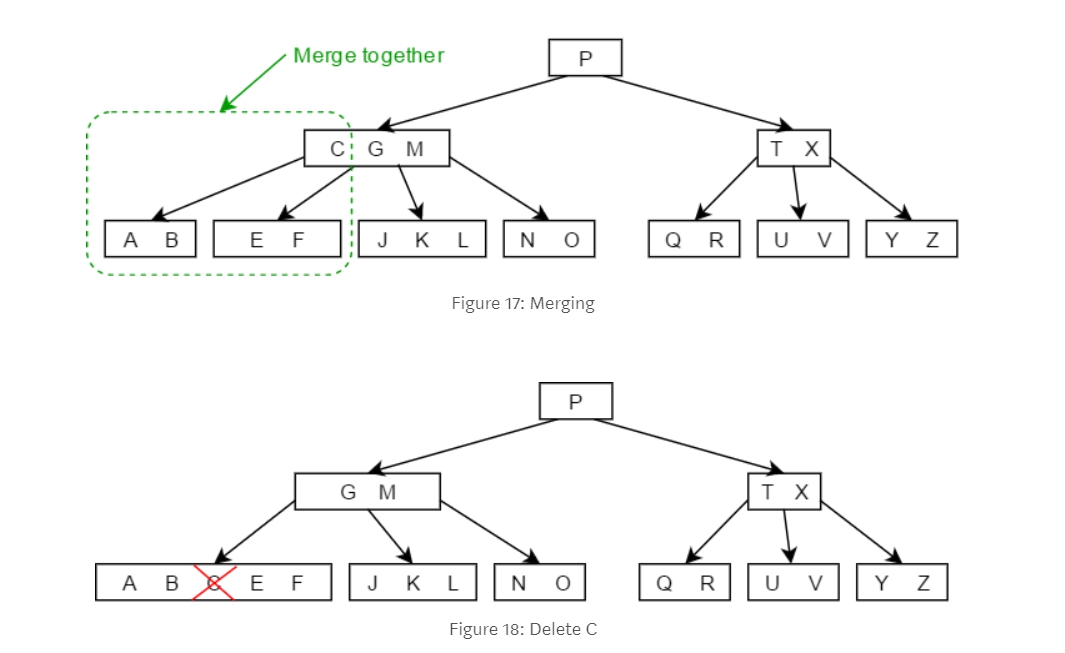
資料含量
首先我們要知道一個Node又稱作Block,且Block通常都會有預設的固定大小,這就跟我們Degree可以設多少很有關係。而一個Block裡面又會有,Key(資料鍵)、Data Pointer(pointer指向資料位置)、Chidren pointer(pointer指向children node位置)。